Privacy-preserving smart contracts

We define a privacy-enabled smart contract as an executable code that can work with both private (accessible by the user only) and public (accessible by everyone) information. Unlike solidity smart contract in EVM based chains, we want to keep and process users' private data (private state) on the user's side. This data should not leave the user device ideally, because private state may hold highly confidential data, like KYC credentials, secret notes, identities, etc. The Public state is designed to hold the data accessible by all users at the same time (low confidentiality data).

As far as we have 2 different levels of confidentiality, an access control system is required to manage how data from different levels could be accessed and written. The basics of the security model intended to enforce access control in the State-transition systems (that blockchain essentially is), which preserves confidentiality on different levels, were defined initially by Bell and LaPadula in their famous BLP model and its extensions. This model mathematically defines the “system”, its state and transition relations so that if the initial state is considered secure, then each subsequent state is considered secure as well. Referring to the initial description, the system Σ(R,D,W,z0) ⊆ X × Y × Z is defined by (x,y,z) ∈ Σ(R,D,W,z0) if and only if (xt,yt,zt,zt,-l) ∈ W for each t ∈ T, where z0 is a specified initial state usually of the form (φ,M,f), where φ denotes the empty set. Practically, this model defines one discretionary access control (DAC) rule and two mandatory access control (MAC) rules with three security properties:

• The Simple Security Property states that a subject at a given security level may not read an object at a higher security level.

• The * (Star) Security Property states that a subject at a given security level may not write to any object at a lower security level.

• The Discretionary Security Property uses an access matrix to specify the discretionary access control.

Visually, this could be represented with the following diagram:

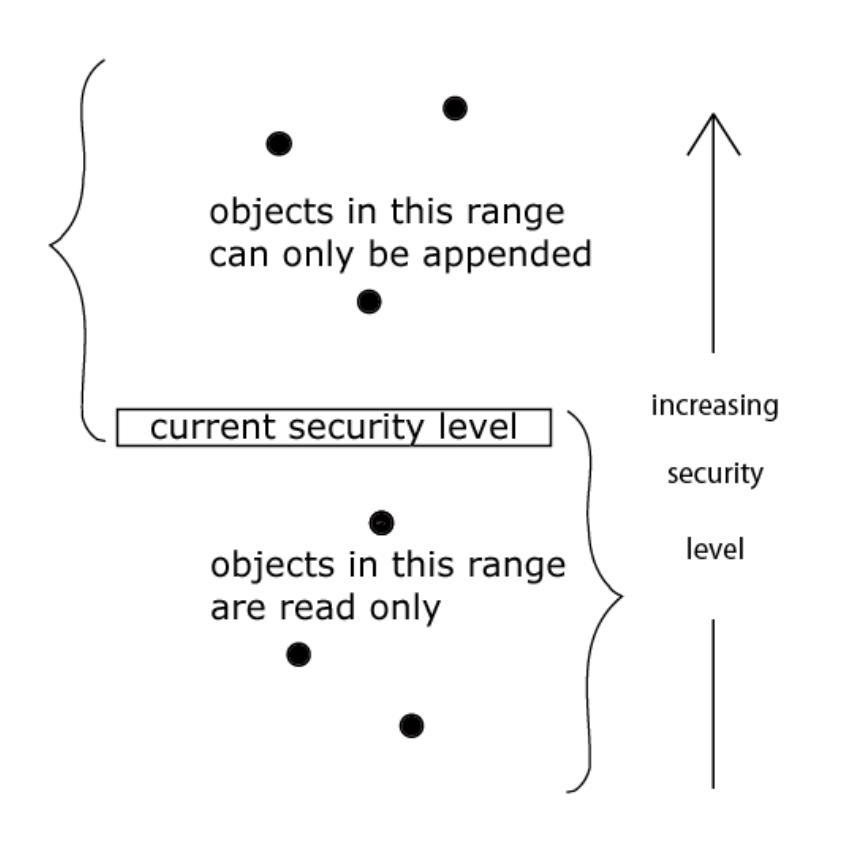
In our particular case, we have 2 levels of confidentiality: Private and Public, so according to the BLP model, we’ll have the following DAC matrix:

	Into/from Object in private context	Into/from Object Public context
Subject in Private context can	read/write	Read
Subject in Public context can	append	read/write

More complexion arise when we put the following statement into the equation:

1. Public state is shared between all the users, system to keep it in consistent state

2. Private state is NOT shared, meaning that user A doesn’t have access to a private state of user B, despite the fact that they are technically on the same confidentiality level according to the BLP model.

It’s easy to address item 1, because blockchain is essentially a system that was designed to solve this problem, but it’s not easy to address item 2. Unless we employ Zero Knowledge.

The problem of doing computation on users’ side was addressed by Zexe. We will follow the same approach to do computations on users’ private state. According to research by authors of Zexe, private state should be structured and kept in the form of UTXO with defined state transition rules, that will result in adding new state as ZK Note and nullifying previous state with appropriate Nullifier, likewise it was defined in ZCash paper. This way an execution of a function (or computation) looks like:

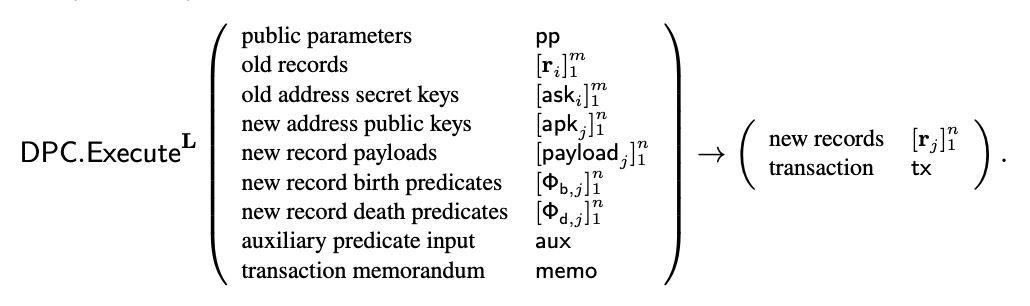
Given as input a list of old records with corresponding secret keys , attributes for new records, private auxiliary input aux to birth and death predicates of new and old records respectively, and an arbitrary transaction memorandum memo, DPC.Execute produces new records and a transaction tx. The transaction attests that the input records’ death predicates and the output records’ birth predicates are all satisfied. The user subsequently pushes tx to the ledger by invoking L.Push(tx).

On input public parameters pp and a transaction tx, and given oracle access to the ledger L, DPC.Verify outputs a bit b, denoting whether the transaction tx is valid relative to the ledger L.

This approach guarantees that private state data doesn’t leave users device, the only thing that is transferred back to the blockchain node is the proof that computations were a) performed b) completed without errors.

From the system security point of view, it breaks what BLP model defines (because proof is essentially a result of computation on Private confidentiality level, which should not be written to or accessible to a code (a subject) on a lower level of confidentiality). But, as far as this proof doesn’t explicitly contain any information stored in private state, this is considered acceptable from the security point of view. The only point of concern that is left is whether or not such an approach allows for creating and exploiting Covert Channel by providing an arbitrary computation algo and receiving a computation proof. This point can not be properly addressed until practical implementation emerges, but when it does, we’ll follow the U.S. Government published guidelines for covert channels in secure systems they certified: “Covert storage channels shall be treated as follows:

• There shall be no covert storage channels with a capacity exceeding 100 bits/second;

• All covert storage channels with capacities exceeding 10 bits/second shall be auditable;

• All covert storage channels with capacities exceeding 1 bit/second shall be described in the product’s covert channel analysis.”

From a practical perspective, in our system, obtaining proof is equivalent to 1 bit of information. Computing a computation proof on the user's side, from different functions, requires these functions (in a form of smart contracts) to be deployed first, then invoked by the user. This doesn’t seem practical in terms of reaching 10 bit/second rate at least as of current system design and understanding.